|
“Estrella” - composition analysis |
|
Ggeoglyphs in the Nazca mountains - is it just a simple ornament or the plan |

|
Chapter 1. Informative and semantic features |
|
© V. Kulikov |
|
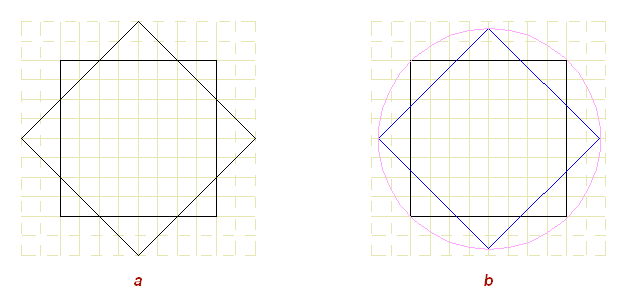
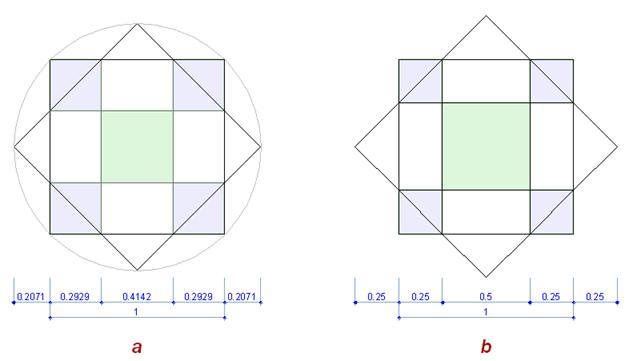
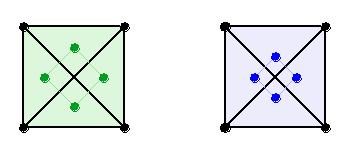
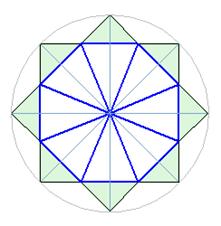
First of all, lets note, that we have the eight-pointed star, which differs from the "regular" eight-pointed star, by ist consistance of the different sized squares. This could be explained by the fact, that our formulation is based on a modular rectangular grid. The octagon, formed by the intersection of the squares is not equilateral (Fig.2.а).
Fig. 2 In the regular star (Fig. 2.b), created by the reversal of two equal squares, everything is balanced: the cuted off triangles are equal, and as the result we have a quite regular octagon with 16 axes of symmetry, rotated by the same angle, relative to each other (360/16). These properties are making the regular star closer to the circle.
|
|
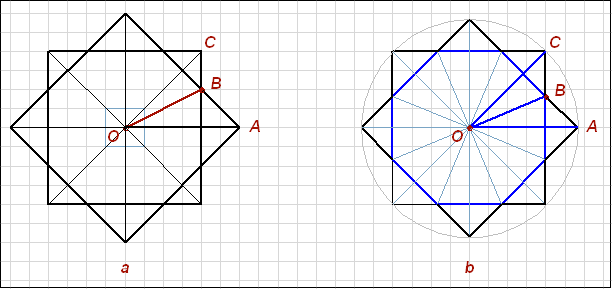
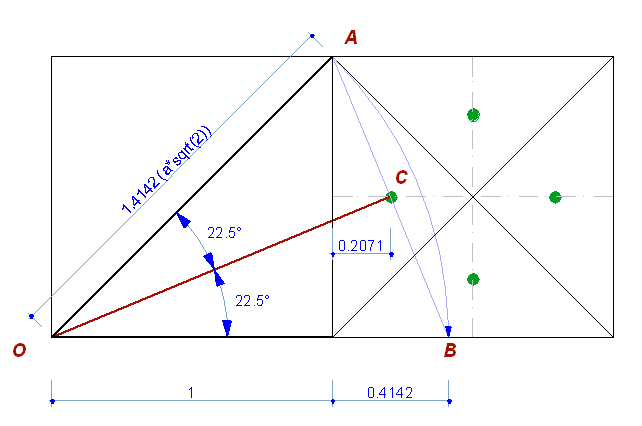
The rest of the geometrical shapes - has a problem. There are two options:
Fig. 5 In the first case, we are following the rule of the general composition, but facing with its disadvantage: the angle AOB is not equal to the angle BOC. (Lets increase the central part.) Fig. 6 Because of the inaccuracies of the geoglyph pattern, it is difficult to distinguish exactly which version it corresponds. The star in different versions would look almost the same. But this fact was also taken into account. Below is shown the geoglyph with the marked points, and the ray, passing through them.
Fig. 7 The point lies in the middle of the height of the cell, but offset from its vertical side.
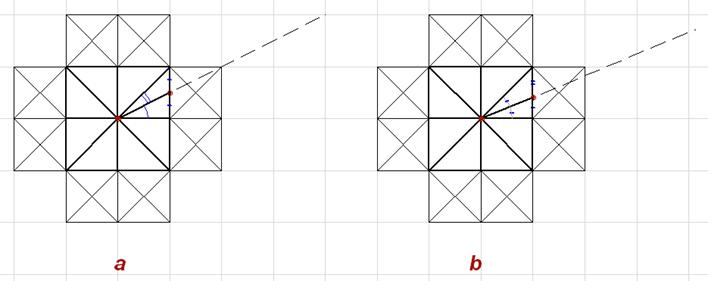
Fig. 8 This division of the angle into equal parts is used while constructing the 16 rays of Estrella. Thus the angle of a regular octagon is formed, but in our case we have an "orthogonal" octagon in the basis of the regular star. This fact contradicts the logic of the of the orthogonal modular formular of the general composition, but projects the same logic (division by 2) on the radial system. Thus, the polar system is added to the general composition of the geoglyph. There is a conflict (in contradistinction) of two different geometrical systems: the regular octagonal star, created on the principles of the polar systemand and "irregular", created on the principles of the orthogonal modular basis. And what are the other three points for ? Forming a diagonally angled square, they show that the points are located exactly on the middle axis of the cell, not closer or farther to the top. The diagonal crossings of the cells are also helping to understand the inaccurate picture correctly. The fact is, that the markings (in this case) are applied in order to indicate that the angle is bisected by the rays, not the side of the cell, as it could be assumed, following by the logic of the general composition. Otherwise, it could be enough to stop the ray on the side of the square, while constructing the bisector, or, in the extreme case, to bring it to the first point. But we have just four points, which are associated with the square, with the help of which the rules of construction are easy-to-read. The marking points on the composition, are not accidental and not for aesthetic purposes. They are created for refinement of the drawing, guaranteeing the correct reading of the general Estrella scheme. Almost the same value of the angles, obtained in different versions, can cause a mistake while reading the scheme, and, with the expectation that changes in the logic of drawing can not be seen at once, lets focus on this moment. The points are showing that the rules of the "regular eight-pointed star" are correctly working in this part of the drawing. This indicates that fact, that the drawing has the properties of illustration, i.e. it is drawn to be readed. The markings, as the semantic elements, are used as the explanations for the drawing. But whom all these explanations are intended? And why the question "are these angles the same or not?" is so important? Is "the problem of constructing the rays" the only one problem, or the drawing contains much more information in itself? The conclusions, concerning the illustrative nature of the markings are confirmed by the following:
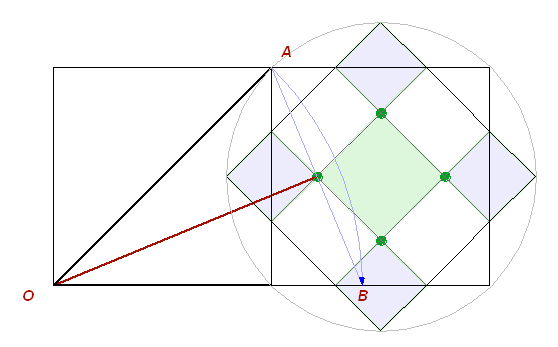
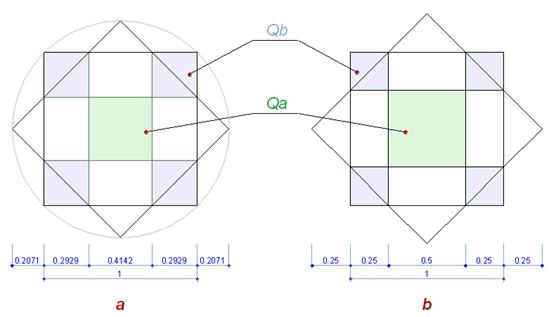
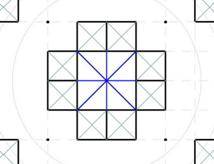
Fig. 9 At the intersection, there are two rotated squares form a regular octagon (Fig. 9.a), with a side equal to sqrt(2) – 1 (with the side of the square = 1). The regular octagon is based on the proportional ratio of the square side to its hypotenuse, which is expressed through the sqrt of 2. The division of the square into the irrational parts by the vertices of the octagon is going on, according to the same proportional factor . (And the area of cutted off triangles is equal to the area of the middle square, marked green). In the modular orthogonal star, the division of the square is going in line with the modular grid (Fig. 9.b). The sides of the blue squares are exactly half the sides of the green square. (The sum of the areas of the blue squares is equal to the area of the green square).
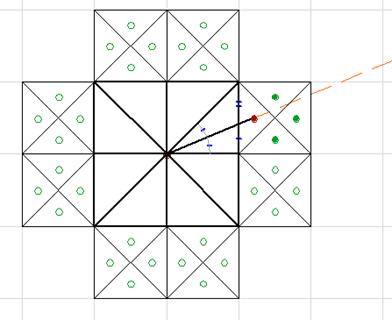
Fig. 10 The points in the cells of the geoglyph are corresponding to the irrational square cells of a regular octagon. Lets try to guess - where are the smallest blue squares are used?
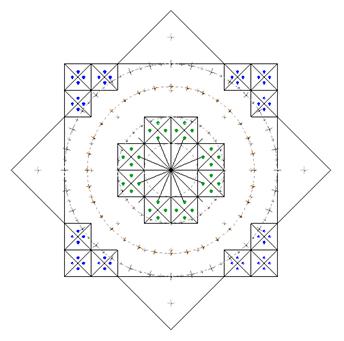
Thus, the cells can be divided into four types: first of all - empty and marked cells, then - marked by the large square Qа and the small square Qb. Fig. 13 In the irregular star the proportions of the matrix are adapted to the modular ratios:
Fig. 14
We see that the matrix Qa-Qb of the squares, shown on the (Fig. 14), is included in the composition, as a system of proportional ratios of the regular octagon, used for the construction of the 16 rays. It is also serves as a scheme for marking the cells, thus connecting the rectangular and polar systems together. The location of marking cells once again brings us to the fact, that we are talking about the relations of the polar and orthogonal systems. What we have as the result? The radial geometry of the system takes its beginning from the center of the star, and in the result we have rectangular star, subordinated to the rules of the orthogonal modularity. It is much easier to imagine, that ancient artist could depict the ducks in the corners and the boat in the middle. But to create a complex square with a side, related to the side of the cell in the proportions of radial system, and enjoy how it looks, spreading it around the circle in the rectangular system as the intricate dots - impossible to call just an amusement. So the location of the marked cells and the size of the marking squares - are the direct features of the inclusion in the general composition, built on a modular orthogonal basis of the elements of the radial system of the regular eight-pointed star. It alludes both on the proximity of these systems and on their differences, what fundamentally change the internal properties of the composition. The presence of these internal connections between the elements, convinces me that the geoglyphs is created for the informative purposes. The technology of these harmoniously working "elements-hints", included in the general scheme for serving the role of directional signs, is not typical for the traditional methods of presentation of the information, by the mathematicians and philosophers of the ancient world. The aesthetic component is only a canvas, the basis for the presentation of information, like the wordplay in a poetic manner, carrying the layers of deeper meaning, not revealing in the specific words. Lewis Carroll, probably, got pleasure by packing mathematical puzzles into the funny poem for a little girl. But he had an appropriate education. Each element, included into the general composition of Estrella - is the significant carrier of some information, a symbol of a certain geometric language. |
|
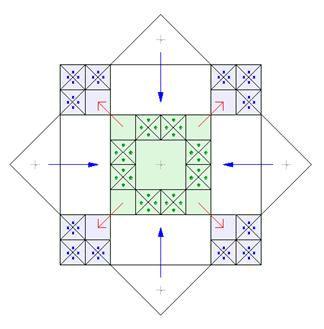
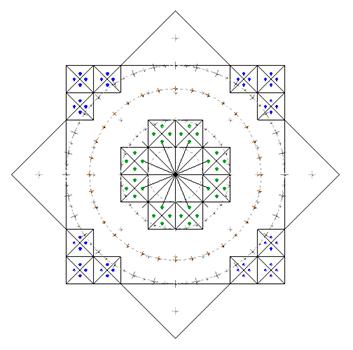
Lets single out the main components of the composition: ¨ Marking points. (Marking squares, formed by 4 points, which are represented by the circular holes in the ground). ¨ Their marked cells are marked by squares and crossed diagonals. ¨ 16-pointed star in the center. ¨ Concentric circle. The circles are divided into successive division by two. The big one is divided into 32 parts by the large dots. Then each segment is divided by two, by the smaller dot. So, we have total - 64 parts.
|
Рис. 1 |
|
Рис. 3 |
But there is one drawback: the regular star doesn't fit a modular grid. Length of the side of the octagon, as well as the length of the sides of the triangles are the irrational numbers, based on the infinite number in the fractional part sqrt(2). (In other words, it is difficult to draw it with a pen on a squared paper). This feature separates it from the square of orthogonal system. In modular rectangular system the equal values are arranged parallel to the axes (not around the circle, as in polar systems). The square and the equilateral triangle - are two regular shapes, that can be divided by the simular shapes without the rest. In other words, the internal space of these shapes could be completely filled with the similar shapes, with the multiple size. This fact gives these shapes an important property - modularity, defining the parameters of their internal space. Each component of such a system can be self-similar system.
|
|
Рис. 4 |
Lets turn but back to the patterns.
|