“Estrella” - composition analysis

Chapter 2. Nested or recursive system

© V.Kulikov

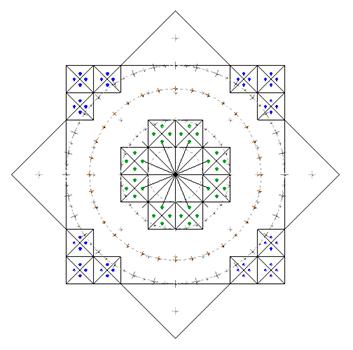
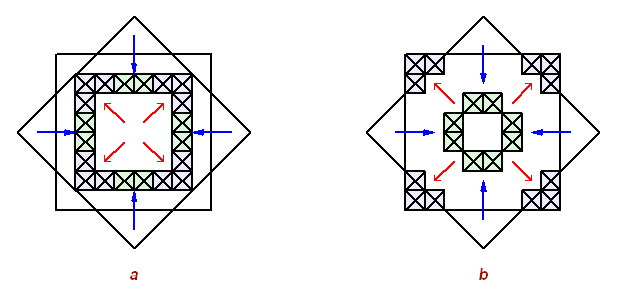
Fig. 1

With the addition of the circles, the system gets a new impact for the deformations. On the background of the circle, the weakness of the orthogonal system against the symmetry is forcing it to modify its internal structure of the elements by adding new rules in their relations.

Let's try to look at another layer of our composition. 

Lets recall, that the regular star with its radial properties is more closer to a circle than to a square. Without the apex of the triangles the square turns into a regular octagon. All its sides are equal and equidistant from its center. Actually we can quite easily convert a square into the shape close to a circle, but at the same time we shall lose its essential quality - modularity of the rectangular elements of the internal structure. Thus, the square loses its advantages and its component parts become not multiples of each other in size, as well as to the square itself.

Fig. 2

With the preservation of the modular structure, the square will get closer to a circle: with the decreasing of the cell size, the ability to create a variety of the equidistant from the center elements - increases.

In other words, the usual sampling (quantization by level):

Step by step we divide the cells of the square in a half and cut off the cells, which are not belong to the circle.

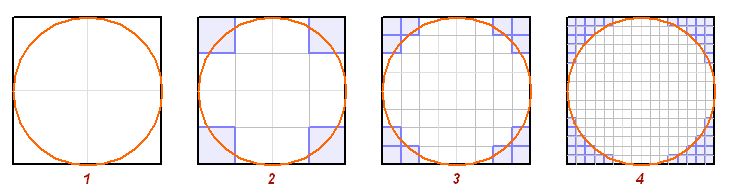
Fig. 3

Lets pay attention to the Stage 2 and 3 of the repeated process of dividing the modular cell.

Stage 2 - this is our matrix Qa-Qb (Fig. 14.b. Ch. 1.), taken from a regular octagon. The squares Qb are appearing to be outside the circumference border.

Stage 3 - the development of our process by cutting off the extra squares in the modular grid equal 1/8 of the square side, but this is also the main square of the geoglyph star as it shown on Fig. 1.

In order to keep the balance and order, lets add the missing squares Qa, and see how they will behave in the process:

Fig. 4

Stage 3 (8x8) - just awesome. It contains all of the previous (4x4 - Stage 2 and an empty 2x2 square - Stage 1), and shows us the "mechanism in action".

The process can be endless. As a result, the square will "fit" its cells up to the circle border with more accuracy with each iteration. This is the property of the fractal systems.

The marked cells are showing the important property of the system, which is called - the structural recursive. (When the self-similar structure is working at all of the levels). In addition, we watch the alternation of negative (inverse) changes on each stage: void is replaced by the marking on the next step.

So the "zoning meaning" of marking cells reveals:
Qb - is the quantums of the square space, being cut off by the "centrifugal" forces. The "centripetal" elements Qa are satisfying the terms of the equidistance from the center.

Or in other words: Qb - is an expansion zone, Qa - ia a compression zone.

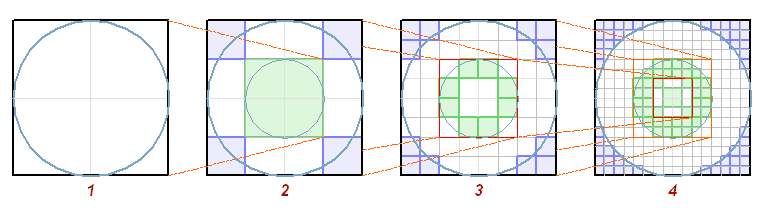
Fig. 5

The fact, that the composition is consisting of the elements, which are identical to the structure of the general composition, indicates on its recursive properties. The fact, that nested compositions are representing that very general system at the previous stage of its development, indicates on the internal dynamics of a fractal process. The result of this process could be a certain goal, located "beyond the infinity".

For example: The number of the cells inside the circle will seek to the circle area, and the number of adjoining outside cells will seek to the outside border of the circumference. These values ​​are associated with the linear size of the circle radius by an irrational number Pi, and therefore the exact result is impossible in this case. The process, directed to the infinity by means of dividing the modular grid, will approximate to the true circle with each iteration.

I think this is a very important layer of the drawing. If we assume that it is also has an illustrative finction ( from the inheritance of the parent process), we can make the following conclusion:

The drawing is representing itself the repeating processes of specification or discretization, which are endlessly approximating to the infinitely remote solution.

According to the general rules, working within the system, it means, that other elements of the system should be considered within the dynamics of the repeatable processes.

The composition contains the items, which are existing in the direct relation between each other. The rays, the marking dots and the marked cells are the members of the same compositional theme. Is that a simple coincidence? Being superimposed on a single logical basis, it can not be just a coincidence. The clearly defined "sign function" of the auxiliary elements of the scheme tells us, that someone wanted to draw our attention to the reading of geoglyph's geometry. To speak of Estrella, as about just an aesthetic research in the field of "geometric ornamentology", is very, very difficult.

I feel ill at ease to write about the discretization of a fractal approach, examining a group of geometric primitives of the primitive times. Who could so easily manipulate with the multi-level geometric concepts, placing ten-meter crosses in the cells, on the distances of several hundred meters? Who is that "someone", who was trying to illustrate something, so deeply taking care for it's understanding? ..

Whether all these coincidences are occasional? I just try to follow what I'm am seeing by my own eyes. It's like finding a figure of the Bear among the billions of stars. But the geoglyphs provides many regularities, and some of them are brighter and grouped in a certain lines, thus making this "Bear" to became a volumetric model, walking around us. Of cause, one can regard it as a pleasant hallucination, but it seems to me, that one better pick up his legs, not letting this Bear accidently to step on his foot.

Ggeoglyphs in the Nazca mountains - is it just a simple ornament or the plan
of the Great Pyramid?