In Chapter 1 we have learned, that one of the main rules of the Estrella drawing is a the successive division by 2. In the rectangular system, we divide a cell into squares, in the polar system - the full circle. The square 8x8 and 16 rays are representing the third stage of this process (2 ^ 3). The signs of the previous steps (division by 2 and 4) are also present here. It indicates on the internal dynamics and possibility of the process continuation (division by 16, 32, 64, and etc.).
Lets consider another feature of the middle part of the scheme:
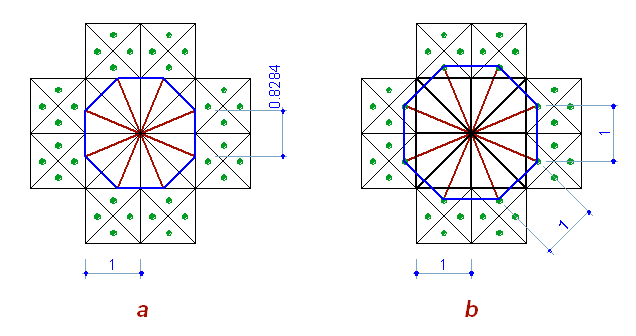
Fig. 1
The rays of the third stage, intersecting the sides of the cells (Fig. 1.a), are forming a regular octagon. (It would seem - everything is enough beautiful, what more do you need? Why do these rays are extended beyond the borders of the square?)
But we see, that these rays are extended up to the marking points (Fig. 1.b). Thus we receive an octagon with a side equal to the side of the cell!
The perimeter of the octagon is equal to 8, or:
a.) to the perimeter of the 2x2 square, which is surrounded by the marking cells.
b.) to the side of the main square (8 cells).
But the polar system, as we have already told, is committed to the circle. Hence, consistently increasing the number of sides in 2 times, the polygon will be closer to the circle. And keeping the relation with the orthogonal system (when the side is multiple to a module), we will get a circle with a circumference of modular square!
In support to this conclusion, se the scheme below. The geoglyph has a circle, divided into 32 parts (R = 2), and the largest circle of the geoglyph (R = 4) is divided into 64 parts:
|

Fig. 2
|
By combining the rules of both rectangular and radial systems, we get the matrix (Fig. 1.b), connecting the circle and the square with the same perimeter.
Eight marking cells, connected with the radial rays of the system, are representing the relation between the both opposite systems - radial and orthogonal. This relation is coming through the perimeter of the circle and the square. Eight square cells are located in accordance to the equidistant tops of the octagon. Very elegant illustration of the dialectical structure of the Universe. The problem of squaring the circle, apparently, was not just an attempt to solve a simple task of calculating the perimeter of a circle. The tend of the circle and square to each other, finds a solution in the perimeter equation, where the properties differing these two figures, become the additions, which finally run both systems together. But this solution appears, like a point of intersection in the endless process of the aspiration. This point is momental and multi-time, as well as the state of the Space quantums, which are dividing and uniting again in accordance to the rules of their System.
But we are talking about the geometry ...
|
Thus, the "star" shows the relations between the circle and the square, and a mechanism of the successive approximation to the point, where the perimeter of the circle is equal to the perimeter of the square. And as the division by two is endless, this point is unattainable. This relation is expressed in modern mathematics through the ratio of the diameter of the circle to its circumference, and it is called - the irrational number "Pi".
The most surprising fact is, that there is no any evidence on the dependence of the circumference length in the form of any integer ratio. Here, in our case, we see the mechanism of the successive approximation.
Concerning the history of "squaring the circle", this decision is weird, taking into the account, that the attempts to date the geoglyphs are ranging in the interval between 500 B.C. to 500 A.C. Although this dating is applied to the Nazca tribes, who inhabited in this territory, and as far as my opinion is concerned, it has no any relation to the time of geoglyphs creation.
In ancient times, the ratio of the perimeters (or areas) of the circle and the square (Pi) was to expressed in the form of an integer ratio (rational numbers). In other words, the number Pi was represented as a fraction (256/81, 4 * (11/14)). In ancient Egypt, as it seen from the mathematical papyri, there were attempts to calculate the slope of the pyramid faces, using the slope of the hypotenuse of a triangle in 5 1/2 or 5 1/4 seked. But papyri belong to much later period, taking into account the fact, that they are copied from the ancient documents, which, in their turn, are also belong to the period much later, than the real time of the pyramid construction. And there is no any indication, that this is related to the circumference of a circle. All these attempts - are the integer ratios.
By constructing a number of regular polygons with sides 6, 12, 24, 48 and 96, Archimedes made the conclusion, that 3 10/71 <Pi < 3 1/7. It is the first attempt to build a consistent approach, an attempt to create an algorithm of approximate calculation. But with a help of it, he tried to find the ratio of integers equal to Pi.
Then, the mathematition for several centuries were searching for a more close relation .
Only in the 17th century, G. Leibniz has proved, that Pi - is an irrational value, and that it is impossible to imagine it as the finite fraction.
The polar system forms a regular polygon with a side, corresponding to the size of the modular cell at the same stage of division by 2.
So, with the gradual development of the general composition, we must get the polygons with the side, equal to the cell of the module system, by increasing the number of sides as a power of 2. And its perimeter will be equal to the perimeter of the square.
Thus we just need to learn how to use the polygon matrix (let's call it so).
To do this, lets watch the changes of the polygon in the stages of the system development.
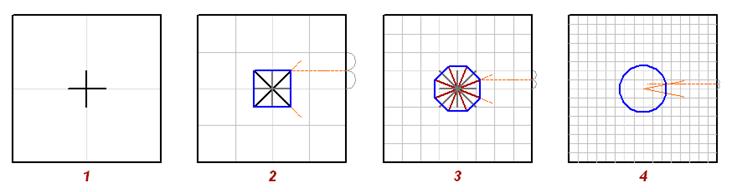
Fig. 3
|
Stage
|
The division of the modular grid on:
|
The number of symmetry axis of the polar system:
|
The division of the circle into:
|
The number of polygon sides
|
|
1
|
2
|
2
|
4
|
-
|
|
2
|
4
|
4
|
8
|
4
|
|
3
|
8
|
8
|
16
|
8
|
|
4
|
16
|
16
|
32
|
16
|
So, we get the rule of the polygon construction:
The vertex of the polygon on each stage is determined by the intersection of the new ray with the line, passing through the middle of the modular cell (Fig. 3.2).
The perimeters of these polygons are equal to the side of the main square.
Similarly to the polar matrix (Chapter 1. Fig. 9), the polygon matrix, increased in its scale up to the size of the general composition, will generate a series of polygons with a perimeter, equal to the perimeter of the main square:
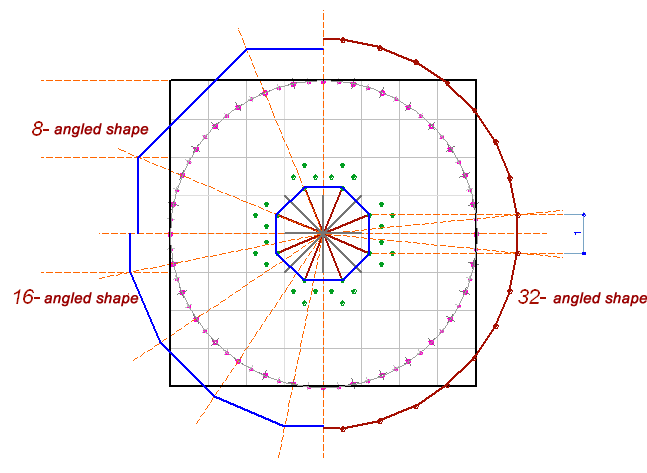
Fig. 4
This step involves 32 marking points of the big circle. The total number of points - is 64.
In addition, the octagon side, shown on the Fig. 4 equals only to a half of the main square. The expected development of this scheme could be up to 64 polygon, with the side, equal to the cell of our composition, and the perimeter will be equal to the perimeter of the square 16x16:
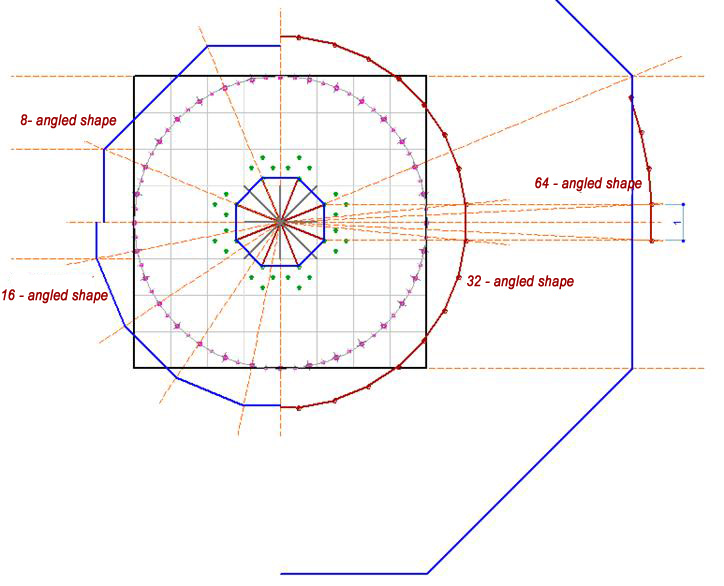
Fig. 5
So, we get the instructions for operating the "polygons matrix":
For receiving the series of polygons, tending to the circles of the given square, we need to scale the matrix up to the size of the square and then to "run" the mechanism of successive division of the systems by two. :)
Thus the matrix of the polygon can generate a circle with a perimeter of the given square.
The side of the octagon, built with the help of a matrix on a square 16x16, will be equal to 8, i.e. to the basic square of the composition. The distance from the center to the vertices of the obtained polygons will tend to the radius of the circumscribed circle. The 1/8 of the perimeter of this circle will also approach to this length.
So, the division of the circle into 64 segments, leads the system to the creation of the circle with the perimeter of 64.
In addition, the initial phase of construction - the octagon, is the polar matrix for our star:
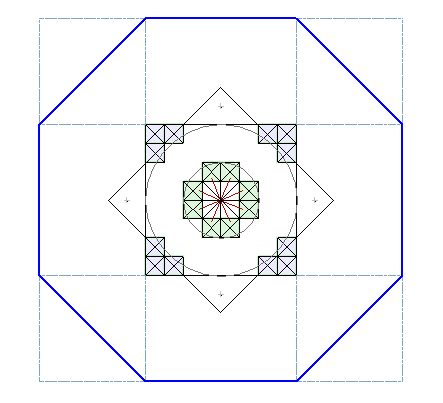
Fig. 6
16 rays with the marking points on geoglyphs are demonstrate the following rule:
While the sequential division of the square and the circle by half, by crossing the lines (which divide the square) with the axes (which divide the circle), we get the points, which appear to be the vertices of the polygon. The sides of this polygon are the multiples to the sides of the square, and its perimeter is equal to the perimeter of the square.
This star demonstrates not only the contradictions, but also shows the relations of the square and the circle. And not just any simple relationship, but the specific points, where two different systems overlap and work together. The octagon, the result of the intersection of the two squares, is the link between the square and the circle, the cube and the sphere. It is the link between the two completely opposite geometric systems - orthogonal (2D or 3D) system and a polar or radial system.
So we have the mechanism of approximate calculation of radius of the circle with perimeter, equal to the perimeter of the given square. We have the mechanism, working not according to the particular rule (e.g. 355 horizontal and 113 vertical), but according to the specific algorithm, with a help of which it is possible to achieve any desired accuracy, by means of repeating process of dividing by 2, thus creating the next polygon.
The logic of the recursive composition determines both internal and external development of the process. The star, packaged in an elegant geometry, containing the rules, which run the system on equalization of two opposing entities.








