Chapter 4. Circles and their perimeters.

“Estrella” - composition analysis

Ggeoglyphs in the Nazca mountains - is it just a simple ornament or the plan
of the Great Pyramid?

Chapter 4. Circles and their perimeters.

V. Kulikov

Now, using the previously discovered logical vectors and compositional patterns of the system, lets try connect to the general "machine" the remaining elements of the geoglyph - two groups of concentric circles, located outside the star. The geometry rules of the star will find their confirmation again in the new interesting "coincidences".

First, a bit about the "rules."
Two "anomalous" objects are located outside the main star, next to it. At the first glance, they do not have any connection with the precise geometry of the main star.

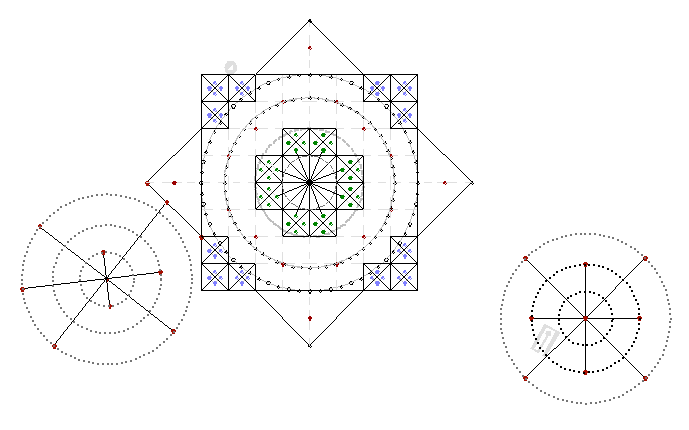
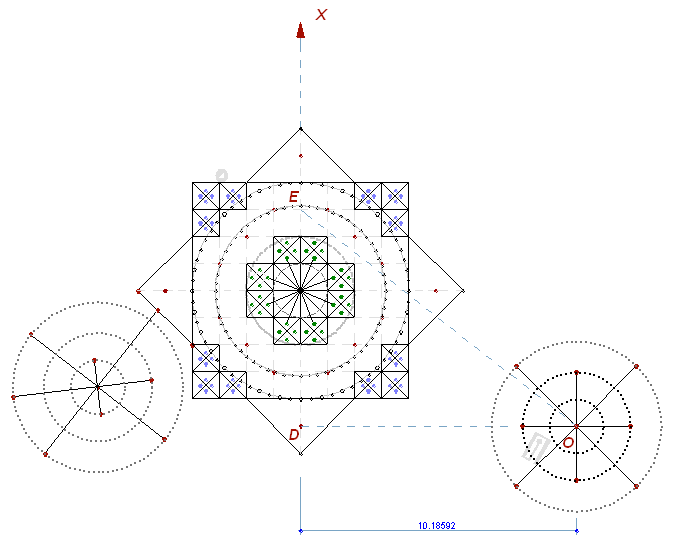
Fig. 1

It is striking that the circles have the same radius, as we see inside the main star, and are placed on the coordinate axes.
In contrast to the circles of the main star, the scaling divisions, forming the circles of these two patterns, are irregular or not accurate. The circumferences are represented by the sequences of the dots (pits on the ground) forming the circles.
Furthermore, as the representatives of the polar system, they are interesting from the standpoint of their geometry:

	Radius	Perimeter	Area
1	1	2 * Pi	Pi
2	2	4 * Pi	4 * Pi
3*	Pi	2 * Pi²	Pi³

* After the careful study of the pictures, we see, that the third circle, both inside and outside the star, is slightly more than a circle with a radius of 3. So I assumed that the radius is equal to Pi. For the present time, I do not see what it can influence on further, then more "interest" occurs, as it looks like a photographic reality.

Why "Pi" again? This number is the transmitting coefficient between the polar and rectangular systems.
We see the circles with the "typical" radiuses. One of the circles has area, equal to Pi; the other one has perimeter and the area are equal to the perimeter of a square with a side, equal to Pi; the third one has an area, equal to the volume of a cube with a side, equal to Pi. Taking into account the multicomplexity semantic combinations of the geoglyph composition, appears an assumption, that the appearance of these circles is associated with their perimeters and their relation to the sides of the squares.

Splitting the circle on the number of segments, equal to the number of divisions on the sides of the square (as well as the polygon with the same number of sides), suggests the idea, that the circle segment is associated with the division of the square side. A quarter of the arc corresponds to the side of the square, and etc.

Thus, the circle deployed in a straight line, will be of a four-length of the square (with the corresponding perimeter), or eight-length of the octagon, or etc.

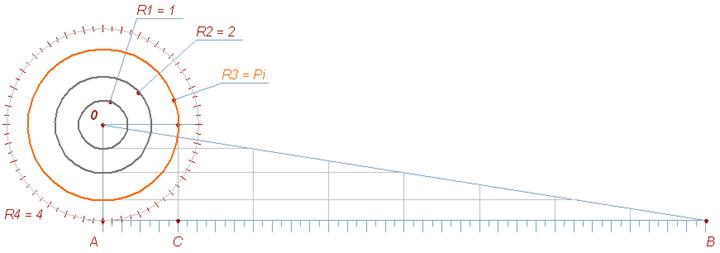
Fig. 2

Fig. 2 AB = 8 * Pi = 25.1327412287183459077011470662360230735773551950008465677995567 ...
AC = π = octagon side with the same perimeter, or to a half of the of the square side (the square is not modular).

The 64-gon, built with the help of the matrix , with a modular side, is almost equal to its circumscribed circumference, the radius of which is already known (Chapter 3 ,Fig. 5). For the 64-sided polygon with the sides equal to 1, this radius will be 10.19001. (Circumference will be equal to 64.02572, while the value of Pi - 3.14033). The accuracy is not much high, but if you continue to divide the polygon, you can get any desired accuracy. For example, a 2048-gon shows radius of the circle = 10.18592, perimeter - 64.0003 and the number of Pi with an accuracy of up to 5 decimal points.

Let's draw down the radius (10.18592) from the point "O" , and then lay out the length, equal to 64 modules. We shall get the following:

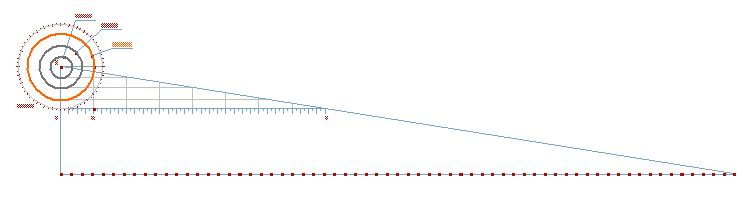
Fig. 3

Here, the segment size (1/64 of the circle) is equal to the modular unit. The correspondence of angular size of the polar system with a modular unit of the rectangular system is established.

Fig. 4

We see, that DE length is equal to 8 units (1/8 of 64), which is the side of our square, or the side of the matrix octagon, shown on the Fig. 22 .

With the help of this "converter", we can find the length of the circle with the required radius. Let's lay out the radius along the axis OD until the intersection with OX. (where DX = 64). Conversely, we can get the radius of the circle with the desired length: lay out the length along the DX and lift up until the intersection with OX. The ordinate of this point will be the radius.

Now - about the coincidence. The location of the circles, located outside the star, satisfy these rules!

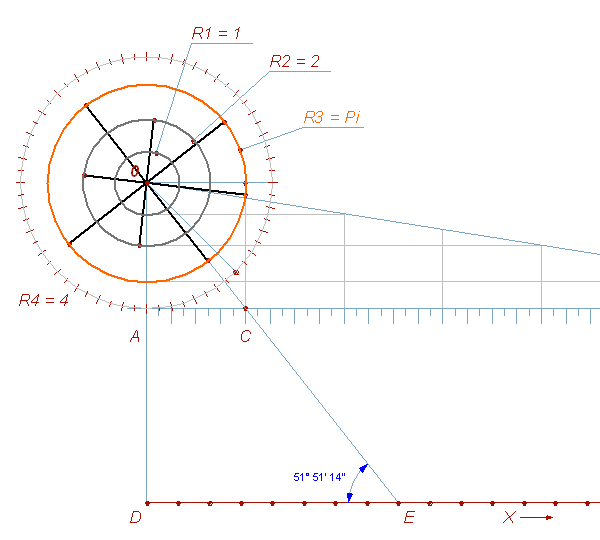
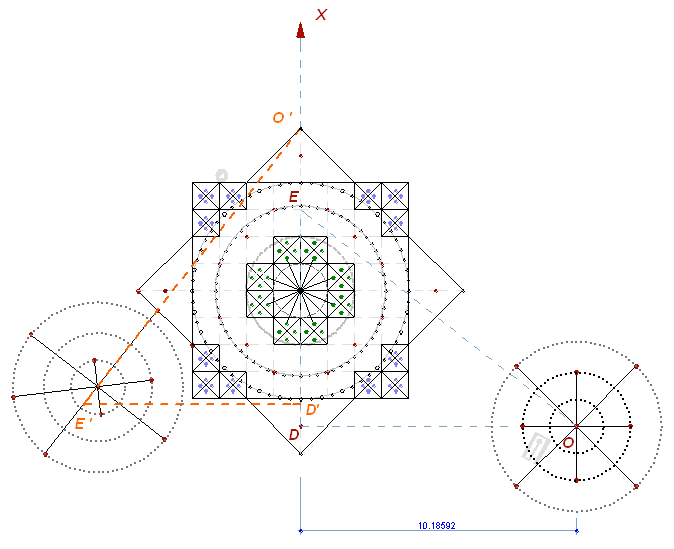
Fig. 5

Here, only the axis have turned. OD = radius of the circle with perimeter of 64, deployed along the DX axis.
DE = 8.

The right group of the circles is fixing the radius of the circle, constructed by the series of polygons on the square 16x16.

Now, let's turn the triangle ODE around point D, and fit O with the vertex, thus receiving the triangle O'D'E ':

Fig. 6

Here, similarly to Fig. 4, E'D '= 8 or 1/8 of the perimeter of a circle with radius O'D'.

The left group of the circles captures the angle that assigns the 1/8 of the circumference (E'D ') and its radius and (O'D').

It is difficult to determine the location of the circles with an accuracy up to 5 decimal digits, just looking on the photo of the geoglyph. But I was trying to check many times the offset OD, and the passage of the ray O'E '. Therefore I can confidently speak about the accuracy to the nearest tenth decimal points (and this is approximately the thickness of the geoglyph's line, what corresponds to the the limit of geoglyph accuracy).

OD - about 10.2 - 10.3 (by module) - can be seen on the air images, taken in the direction, perpendicular to that line. In this case, it is possible to lay out the modul value without perspective distortion. The topographs, in this case, will also cause some distortion along the Y axis, which is not much affect on the distance along the X axis.

O'E '- the passage of the ray through the cells of the geoglyph was checked in details, as well as its intersection with the existing and built geometric lines.

More details, concerning the accuracy of the drawing can be found in the application.

But what for this accuracy? After all, the circles on the pattern do not have any exact binding. Maybe this fact is not accidental? The values, they are pointing on, are variable, depending on the stage of building the polygons. A 32-gon will have one radius, while the 128-gon - another one. It is important to mention, that "here we have the radius of the circle, built on a square 16x16". And the accuracy with which this was done - just a matter of technique.

The same thing with the another circle: it does not have any direct correlation, indicating on the "floating" value, depending on the stage of the system development. But the axis, starting from the point E on the geoglyphs is tied to the only one point. It is drawn up to the side of the diagonal square and confidently goes further up to the point O ', which is the top of the star. Such "binding" can be regarded as an anchoring of vertex of the variable angle E'O'D '. This axis, as well as the line OE, shown on the Fig. 4, is the same variable pointer. It may indicate to 1/8 or 1/4 of the entire circumference or perimeter by changing the angle, but it always will remain at the point O. In this case the ray indicates on the angle, cutting off the 1/8 of the circumference perimeter, the radius of which is indicated by the right circles. And the accuracy of this angle will depend on the degree of precision of the radius of the 64 circumference.

Therefore, we can assume that here we need the following concept:

The circle in the point O indicates on the radius of the circumscribed circle OD with the circle perimeter = 64.
The circles at the point E' are fixing the angle between the radius of the circle, and 1/8 of its perimeter.

The ray O'E ' is cutting the 1/8 of the circumference as:
- the side of the octagon,
- the half of the square side with the same perimeter - very characteristically fits into the overall logic.

The Angle (O'E'D '), obtained in this case, is close to 51° 51’ 14”, depending on the accuracy of the location of the OD radius.
The circles, as well as the marking the points, in this case, are the symbols, that indicating on the important moments of the composition. They are hinting on the Pi and on the relations of this part of the drawing with a polar system (circles and their length).